En el video observamos un trabajo experimental de la caída vertical de los cuerpos.
Para ello se dejan caer dos esferas de dos tamaños diferentes desde la misma altura y se miden los tiempos. Como es de suponer ambas esferas caen al mismo tiempo.
A continuación, hemos cortado con el programa Movie Maker la prueba que nos ha parecido más exacta.
La hemos dividido en fotogramas para poder observar lentamente la caída de la bola.
A cada una de las imágenes le hemos asociado una posición y un tiempo, indicados sobre la imagen.
Hemos obtenido el siguiente resultado:
Con los datos de posición y tiempo hemos construido la siguiente gráfica y-t:
Después hemos calculado la velocidad de la bola para cada posición y su velocidad media para cada intervalo.
Los datos los hemos recogido en la siguiente tabla:
| Posición (m) | Tiempo (s) | Altura (m) | Velocidad (m/s) | Vmedia en cada tramo |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0,08 | 0,025 | 0,3125 | 0,3125 |
| 2 | 0,16 | 0,12 | 0,75 | 1,1875 |
| 3 | 0,24 | 0,27 | 1,125 | 1,875 |
| 4 | 0,32 | 0,49 | 1,53125 | 2,75 |
| 5 | 0,4 | 0,78 | 1,95 | 3,625 |
| 6 | 0,48 | 1,13 | 2,3541666667 | 4,375 |
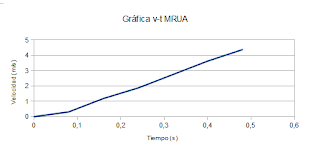
A continuación hemos recogido los datos del tiempo (s) y velocidad (m/s) en otra tabla para después construir la gráfica v-t:
| Tiempo (s) | Velocidad (m/s) |
| 0 | 0 |
| 0,08 | 0,3125 |
| 0,16 | 1,1875 |
| 0,24 | 1,875 |
| 0,32 | 2,75 |
| 0,4 | 3,625 |
| 0,48 | 4,375 |
El movimiento que describe la bola de acero en su caída libre es un MRUA, ya que la gravedad de la Tierra atrae a la bola, aumentando su velocidad proporcionalmente. La aceleración se mantiene contante en -9,8 m/s^2.
En la gráfica v-t se observa un MRUA, lo que verifica nuestras expectativas anteriores, ya que representa una línea recta cuya pendiente es la aceleración.
Así podemos calcular experimentalmente el valor de la gravedad, calculando la pendiente:
La gravedad de la Tierra es de 9,8m/s^2. El valor experimental calculado a partir de la pendiente de la gráfica v-t es muy aproximado al valor teórico, pero no es exáctamente igual porque existe un margen de error humano cometido al hacer el experimento.
Como hemos anteriormente, los datos experimentales no son exactamente iguales a los teóricos, esto se debe a que existe un error humano cometido en la práctica experimental.
Este error puede aparecer en muchos factores, como son:
- La altura desde la cual se suelta la bola puede variar y ser mayor o menor.
- Los tiempos son tomados manualmente y en consecuencia, no son del todo exactos.
- Al dividir el vídeo en fotogramas y aumentar la imagen, se pixela mucho y dificulta la visión de los datos.
- La colocación del metro no es del todo vertical.
- Por último, hay muchos decimales que han sido aproximados.
A pesar de todas estas discrepancias los datos experimentales nos han salido bastante cercanos a los técnicos.

El trabajo tiene un hilo argumental muy bien logrado y hace que aumente el interés por su lectura.
ResponderEliminarLa únicas pegas que le pongo son:
- Lo óptimo es calcular la recta que pasa, en promedio, más cerca de todos los puntos para calcular su pendiente.
- Os ha faltado poner lo cálculos teóricos.
Hemos incluido los cálculos pero no es posible verlos, no entiendo por qué, cuando publicamos la entrada sí se veían.
Eliminar